棱台图片(棱台图片体积)

棱台图片

高考数学一轮总复习第378课：立体几何极易错题！考查不常见的棱台问题，还原法至关重要，来自浙江高考数学试题，涉及线面垂直的证明及线面角的求法，先不给答案了，大家先做做试试，据说出错率很高啊，祝大家学习愉快，加油！

三角函数极值问题

几何问题在国联考的行测考试中出题频率较高，2020年辽宁省考10道题中考查了3道几何问题，因此学好几何问题是十分必要的。
今天我们就来探讨一下几何问题中如何求极值。

一、题型特征：

几何极值问题一般在设问中都有“最大”、“最小”字样。
平面图形一般讨论周长和面积的关系，立体图形往往讨论表面积和体积的关系。

二、解题方法：

一般此类题型可以通过均值不等式或几何极值性质来解题。

均值不等式可表示为：

，当a=b时成立。

几何的极值性质可归纳为：

1.周长相等的平面图形，越接近圆，面积越大。
2.面积相等的平面图形，越接近圆，周长越小。
3.表面积相等的立体图形，越接近球，体积越大。
4.体积相等的立体图形，越接近球，表面积越小。

对于几何的极值性质大家可以分成平面和立体两个方面记忆，尽量发挥想象力理解记忆，避免记错记混。

三、题型考法：

1.利用几何极值性质求解最大面积或体积。

例1用18厘米长的警戒线围成各种长方形，要求长和宽的长度都是厘米数，则围成的长方形的面积最大是多少？

A. 18平方厘米

B. 20平方厘米

C. 25平方厘米

D. 40平方厘米

思路点拨由题意知周长一定，要使长方形的面积尽可能大，则要使形状更加接近圆，也就是让长方形更加接近正方形。
长＋宽＝9厘米，则要求长和宽尽量接近，可使长＝5厘米，宽＝4厘米，此时面积最大，最大面积为45＝20（平方厘米）。
因此，选择B选项。

例2设a、b、c、d分别代表四棱台、圆柱、正方体和球体，已知这四个几何体的表面积相同，则体积最小与体积最大的几何体分别是：

A. d和a

B. c和d

C. a和d

D. d和b

思路点拨根据几何最值理论。
表面积一定的立体图形，越接近球体，体积越大。
立体越对称，越接近球体，则四棱台、圆柱、正方体和球体中，体积最小的是四棱台，体积最大的是球体。
因此，选择C选项。

2.利用均值不等式最大面积：

例3要建造一个新的矩形鸡圈，如图所示，该鸡圈一面靠围墙，另外三面共使用了200米长的铁丝网，问如果想让鸡圈的面积最大，鸡圈的长和宽比值应为多少?

A. 1∶1

B. 2∶1

C. 3∶2

D. 7∶3

思路点拨本题并不能应用几何的极值性质进行解题，因为长方形的周长并不是固定的，需要利用均值不等式解题。
设长为x米，宽为y米，则x＋2y＝200。
长方形的面积为xy，根据均值不等式定理，当且仅当x＝2y时

，

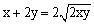
取得最大值，此时长方形的面积最大。
当x＝2y时，鸡圈的长和宽的比值为2︰1。
因此，选择B选项。

四、题型小结：

几何的极值性质其实是均值不等式的简化版，只要多加练习就一定能够熟练掌握。

如何解决几何极值问题,三角函数极值问题

藏区回流老玛瑙鸡骨白十八子配九棱台佛珠项链尺寸：珠子197毫米 九棱台55毫米 厚8毫米 老玛瑙的魅力细想这些年来，走过了山山水水/“玩”过了无数的奇石宝贝/初识时怦然心动，拍案叫绝/拥有后日夜相伴，缠缠绵绵/到最后新鲜感逐渐消散，将它们高置案头/找不到继续玩赏的理由/而唯独只有老玛瑙、这么多年来对它情有独钟将这些在千年以后还可以看到极为美丽的老物件带回家中，好比收藏了一本珍贵的教科书，令人孜孜不倦地阅读，探索其中的奥秘；好比买回一件罕见的艺术品，让人百看不厌，不舍放手；好比结识了一位美丽贤惠的知己，愿与她长相厮守，相伴白头